SUPERCOMPUTING FRONTIERS AND INNOVATIONS
An International Open Access JournalEditors-in-Chief: Jack Dongarra, University of Tennessee, Knoxville, USA Vladimir Voevodin, Moscow State University, Russia Editorial Director: Leonid Sokolinsky, South Ural State University, Chelyabinsk, Russia Production: South Ural State University (Chelyabinsk, Russia) ISSN: 2313-8734 (online), 2409-6008 (print) DOI: 10.14529/jsfi Publication Frequency: 4 issues (print and electronic) per year Current Issue: Volume 10, Number 4 (2023) DOI: 10.14529/jsfi2304. Abstracting and Indexing: Scopus, ACM Digital Library, DOAJ. |
  |
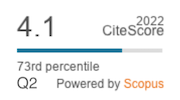 |
- Most Viewed
- Most Downloaded
- Most Cited
| # | Article title | Views |
|---|---|---|
| 1 |
Toward Exascale Resilience: 2014 update
Franck Cappello, Al Geist, William Gropp, Sanjay Kale, Bill Kramer, Marc Snir
|
4008 |
| 2 |
Predicting the Energy and Power Consumption of Strong and Weak Scaling HPC Applications
Hayk Shoukourian, Torsten Wilde, Axel Auweter, Arndt Bode
|
3867 |
| 3 |
Extreme Big Data (EBD): Next Generation Big Data Infrastructure Technologies Towards Yottabyte/Year
Hitoshi Sato, Michihiro Koibuchi, Satoshi Matsuoka, Osamu Tatebe, Ikki Fujiwara, Shuji Suzuki, Masanori Kakuta et al.
|
1726 |
| 4 |
Towards a performance portable, architecture agnostic implementation strategy for weather and climate models
Thomas Christoph Schulthess, Oliver Fuhrer, Carlos Osuna, Xavier Lapillonne, Tobias Gysi, Ben Cumming et al.
|
1408 |
| 5 |
Exascale Storage Systems -- An Analytical Study of Expenses
Julian Martin Kunkel, Michael Kuhn, Thomas Ludwig
|
1393 |
| # | Article title | Downloads |
|---|---|---|
| 1 |
Toward Exascale Resilience: 2014 update
Franck Cappello, Al Geist, William Gropp, Sanjay Kale, Bill Kramer, Marc Snir
|
1394 |
| 2 |
Beating Floating Point at its Own Game: Posit Arithmetic
John L. Gustafson, Isaac T. Yonemoto
|
1100 |
| 3 |
Towards a performance portable, architecture agnostic implementation strategy for weather and climate models
Thomas Christoph Schulthess, Oliver Fuhrer, Carlos Osuna, Xavier Lapillonne, Tobias Gysi, Ben Cumming et al.
|
697 |
| 4 |
Exascale Storage Systems -- An Analytical Study of Expenses
Julian Martin Kunkel, Michael Kuhn, Thomas Ludwig
|
516 |
| 5 |
Extreme Big Data (EBD): Next Generation Big Data Infrastructure Technologies Towards Yottabyte/Year
Hitoshi Sato, Michihiro Koibuchi, Satoshi Matsuoka, Osamu Tatebe, Ikki Fujiwara, Shuji Suzuki, Masanori Kakuta et al.
|
484 |
| # | Article title | Citations |
|---|---|---|
| 1 |
Toward Exascale Resilience: 2014 update
Franck Cappello, Al Geist, William Gropp, Sanjay Kale, Bill Kramer, Marc Snir
|
173 |
| 2 |
Towards a performance portable, architecture agnostic implementation strategy for weather and climate models
Thomas Christoph Schulthess, Oliver Fuhrer, Carlos Osuna, Xavier Lapillonne, Tobias Gysi, Ben Cumming et al.
|
47 |
| 3 |
Beating Floating Point at its Own Game: Posit Arithmetic
John L. Gustafson, Isaac T. Yonemoto
|
35 |
| 4 |
Research Problems and Opportunities in Memory Systems
Onur Mutlu, Lavanya Subramanian
|
35 |
| 5 |
Runtime-Aware Architectures: A First Approach
Miquel Moreto, Mateo Valero, Marc Casas, Eduard Ayguade, Jesus Labarta
|
24 |
